本文对曲线顶管的最重要参数——最小曲线半径进行了探讨,得出最小曲线半径与管段长度、管径成正比,与木垫片厚度成反比的关系。另外还指出曲线半径还受土体承载力的制约,要防止管道在施工中发生纵向失稳。
曲线顶管是顶管的前沿技术,只有当顶管被工程界广泛采纳后才会提出曲线顶管问题。目前曲线顶管各国尚处于研究发展阶段,有些曲线目前已能施工,有些曲线还不能。例如弯曲半径太小,有可能造成管道失稳,管道裂缝等严重后果。曲线顶管多用于旧城区的改造,旧城区马路弯曲,管道一般沿马路敷设,这就需要采用曲线顶管。另一种情况是过江过河的混凝土顶管,有时为了减少投资,把管轴线设计成倒虹管或者抛物线形状,这也需要采用曲线顶管。曲线顶管比较适合于混凝土管。曲线顶管用于钢管,则需要很大的弯曲半径,而且必须有中继环。
管道的弯曲半径的大小与土质、管径、顶力有关。土体承载力高,弯曲半径可以小一点;反之,承载力低,弯曲半径要大一点。管道口径大,弯曲半径要大一点;反之,管道口径小,弯曲半径可以小一点。管段较长,弯曲半径要大一点;反之,管段较短,弯曲半径可以小一点。施工顶力较大,弯曲半径要大一点;反之,顶力较小,弯曲半径可以小一点。
一、 混凝土管最小弯曲半径分析
最小弯曲半径时忽略土体承载力和施工顶力影响,仅就管道口径大小、管段长度、木垫片的厚度三者与最小弯曲半径的关系进行分析。曲线顶管的轴线,从宏观上看是曲线,实际上是折线,是多边形的一部份,多边形的边就是管段长度。从图1可知多边形的边、角、半径有如下关系:
α=l/R
式中 α—中心角(弧度);
l—边长;
R—多边形外切圆半径。
曲线顶管中把管段的长度看成是多边形的边,管段对应的中心角就是多边形的中心角,管轴线就是多边形的外切圆。
假设管道内径为d,壁厚为t,管段长度为l,木垫片厚度为b,并假设管道壁厚是内径的1/10,木垫片允许最大压缩率是50%。
即 t=d/10
S=b∙50%
从图1可知,管段间的转角与管段对应的中心角相等。则曲线的最小弯曲半径可按下式计算:
Rmin=l(d+2t)/(b-s)或Rmin=12ld/5b
式中 Rmin—最小弯曲半径(m);
l—管段的长度(m);
d—管道内径(m);
t—管道壁厚(m);
b—木垫片厚度(m);
s—木垫片最小压缩高度(m)。  由上式确定的不同管径混凝土管的最小弯曲半径见表1。弯曲半径太小,会使管段上应力过于集中,使管道混凝土裂缝。这是要力求避免的。
由上式确定的不同管径混凝土管的最小弯曲半径见表1。弯曲半径太小,会使管段上应力过于集中,使管道混凝土裂缝。这是要力求避免的。
二、钢管顶管的最小弯曲半径
无中继环的钢管不能用于曲线顶管。钢管曲线顶管的最小弯曲半径的大小主要取决于中继环布置的间距和中继环的允许转角。目前钢管顶管沿用的老式中继环允许转角很小,因此不宜用于曲线顶管。组合密封中继环研究成功后,允许中继环有较大的转角,因此可用于曲线顶管。已知中继环的允许转角和间距,钢管管道的最小弯曲半径可按下式计算:
Rmin≥L/2sin(kα/2)
最小弯曲半径参考值 单位:m 表1
| 公称管径(mm) | 木垫片厚0.03 | 木垫片厚0.02 | ||
管段长2.0 | 管段长2.5 | 管段长2.0 | 管段长2.5 | |
| 800 | 128 | 160 | 192 | 240 |
| 1000 | 160 | 200 | 240 | 300 |
| 1200 | 190 | 260 | 288 | 360 |
| 1400 | 224 | 280 | 336 | 420 |
| 1600 | 256 | 320 | 384 | 480 |
| 1800 | 288 | 360 | 432 | 540 |
| 2000 | 320 | 400 | 480 | 600 |
| 2200 | 352 | 440 | 528 | 660 |
| 2400 | 384 | 480 | 576 | 720 |
| 2600 | 416 | 520 | 624 | 780 |
| 2800 | 448 | 560 | 672 | 840 |
| 3000 | 480 | 600 | 720 | 900 |
| 3200 | 512 | 640 | 760 | 960 |
| 3400 | 544 | 680 | 816 | 1020 |
| 3600 | 576 | 720 | 804 | 1080 |
| 3800 | 608 | 760 | 912 | 1140 |
| 4000 | 640 | 800 | 960 | 1200 |
说明:
1.假定土体有足够的承载力。
2.假定顶力在允许范围内。
3.表中未考虑施工偏差对弯曲半径的影响。
式中
Rmin—最小弯曲半径(m);
α—中继环的允许转角,取α=1°;
k—系数,k=0.5;
L—中继环间距(m)。
如果中继环间距L=60m,则弯曲半径Rmin≥6875m。
三、管道的侧向力
曲线顶管的顶力可分成轴向力和侧向力两部分,下面分析作用在管段上的侧向力的大小。由图2可知,折线转向角δ是∠ABC的补角。
因为 ∠ABC=2β所示
δ=180-2β
α=180-2β
δ=α
假设忽略管壁摩阻力,并假设AB管段的轴向顶力是P1,则BC管段的轴向顶力和侧向分力是
p2=p1ctgα
p′2=p1tgα
式中 p2—下一管段的轴向顶力;
p′2—下一管段的侧向分力。
由此可见,曲线顶管存在侧向分力,因此要验算土体的承载力。如果承载力不够,管轴线会因此失稳,侧向分力使管道靠向曲线外侧,并作用在土体上,还会使管道的顶进阻力增加。因此曲线顶管在顶力配置时要考虑管道摩阻力增加的因素。
已知弯曲半径R和管段长度l,就可以求得α。根据轴向顶力的大小,就可求得侧向分力。再根据μ值,即可求得管段的附加摩阻力。

四、顶力的调正
曲线顶进时,管段的允许顶力要折减。折减系数与管段转角有关,混凝土管还与木垫片的弹性模量、木垫片的厚薄有关。曲线顶管不但会使混凝土管的允许顶力下降,而且还会使管道总顶力增加。如果中继环设计顶力不变,则曲线顶管中继环的数量要比直线顶管多。
管道进入曲线段,管段间的顶力传递面靠向曲线内侧(见图2),因此中继环进入曲线段后顶力要调正,使中继环的顶力合力中心与其他管段传力一致。调正的办法是曲线外侧的中继油缸要封住,即部份油缸不使用。停用油缸数量可通过计算。最简单的办法是,观测中继环转角有无变化。转角增加,表示要增加停用的油缸,合力中心还要靠向曲线内侧;转角减小,表示停用的油缸太多了,需要减少;只有当转角不增不减,或者变化不大时,认为调正是正确的。
中继环的顶力调整降低了中继环的实际使用顶力,因此中继环的允许使用顶力还要比设计顶力低,顶力配置时要考虑这一因素。
 五、曲线顶管的超挖
五、曲线顶管的超挖
曲线顶管,要求直线形的管段沿圆弧移动(见图4),因此必然要超挖。超量大小与弯曲半径、管道直径、管段长度有关。超挖量可按下式计算:
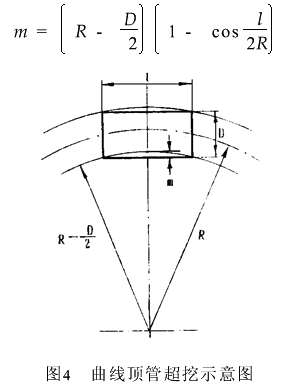
式中 m—半径方向超挖量(m);
R—弯曲半径(m);
D—管道外径(m);
l—管段长度(m)。
例如管道外径2.4m,管段长2.5m,弯曲半径400m,则:
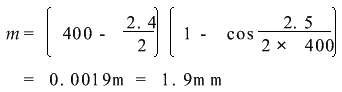
可见混凝土曲线顶管中存在超挖的问题。对硬土来说这是曲线顶进的需要,否则管段很难转向,摩阻力也会因此而增加。对于软土情况就会好一些。所以在硬土中顶管,要考虑超挖的方法。但钢管顶管因为设计的弯曲半径很大,超挖量就很小,可以忽略不计。
六、曲线顶管测量
曲线顶管的测量是曲线顶管的关键技术问题。曲线顶进时因管内外无法通视,因此必须改变常规的施工测量方法,经纬仪必须进管。但管道在施工过程中是不断向前移动的,因此测站的座标也是在不断变化的。要在测站座标不断改变的情况下,随时随地指出管道前进方向,这就是曲线顶管中管道定向测量要解决的中心问题。
解决的办法有2个:
1.管道内布置多台全站仪,依靠全站仪的优势,在短时间内通过计算机确定每站经纬仪的方向,指出管道顶进方向。这一方法实质上是经纬仪导线法,方法可行但成本高。
2.管道内设置一台普通经纬仪,一个觇标,2者均布置在工具管的后部。工具管上的标尺、经纬仪、后视觇标3者间保持一定的距离,并与管道固定,随管顶进而跟进。经纬仪、后视觇标的中心坐标是根据事先测定的实际管轴线计算所得,工具管上的测点座标查设计轴线可得。依靠这3者的关系就可算出管道的顶进方向,并由经纬仪指向。管轴线的测定需要一台全站仪,管道每顶进数10m,测定一次工具管后的管轴线,并输入计算机。施工中可以根据顶进距离,推算出3者的即时坐标,通过计算机的运算,就能指出工具管顶进方向。采用这一方法,速度快、成本低,使用人力少。
上面分析了曲线顶管中的6个主要问题,还很肤浅,尚需各方面共同进一步研究完善。
- 本文关键词: 顶管施工
上一篇:大口径顶管施工出洞技术介绍
